#include <cubicpiecewisefunctionstatic.h>

Public Member Functions | |
| void | evaluate (int outN, double *input_x, double *output_y, double *output_dy=0, double *output_ddy=0, double *output_dddy=0) |
| void | evaluate_ordered (int outN, double *input_x, double *output_y, double *output_dy=0, double *output_ddy=0, double *output_dddy=0) |
| void | fit (double *input_x, double *input_y, double *input_w, double smoothingFactor) |
Public Attributes | |
| double | breaks [N] |
| double | coef_1 [N-1] |
| double | coef_2 [N-1] |
| double | coef_3 [N-1] |
| double | coef_4 [N-1] |
Private Member Functions | |
| void | evaluate1 (int i, int j, double *input_x, double *output_y, double *output_dy=0, double *output_ddy=0, double *output_dddy=0) |
x x x x x x x x <- inputPoints #N x x x x
| | | | | | | | | | | | <- breaks #N. polynomials always between two input/break points y y y y y y <- differently spaced/arbitrary number output points
|
inline |

|
inlineprivate |
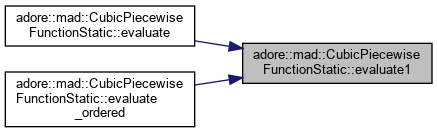
|
inline |
evaluate_ordered is like evaluate, but expects input_x to be an ordered sequence of points. indexing can be greatly improved by this assumption.

|
inline |
based on Schöneberg and Reinsch smoothing spline https://link.springer.com/content/pdf/10.1007/BF02162161.pdf https://en.wikipedia.org/wiki/Smoothing_spline https://wiki.dlr.de/confluence/display/fau/How+to+use+Fit+function size of input_x and input_y has to be N+1
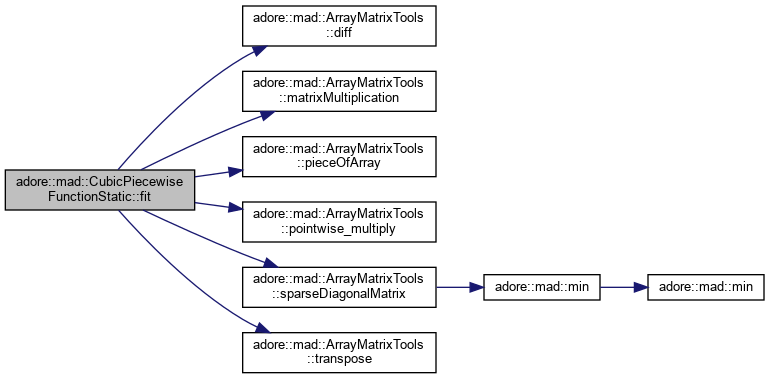

| double adore::mad::CubicPiecewiseFunctionStatic< N >::breaks[N] |
| double adore::mad::CubicPiecewiseFunctionStatic< N >::coef_1[N-1] |
| double adore::mad::CubicPiecewiseFunctionStatic< N >::coef_2[N-1] |
| double adore::mad::CubicPiecewiseFunctionStatic< N >::coef_3[N-1] |
| double adore::mad::CubicPiecewiseFunctionStatic< N >::coef_4[N-1] |