#include <llinearpiecewisefunction.h>

Inheritance diagram for adore::mad::LLinearPiecewiseFunctionM< T, n >:

Collaboration diagram for adore::mad::LLinearPiecewiseFunctionM< T, n >:

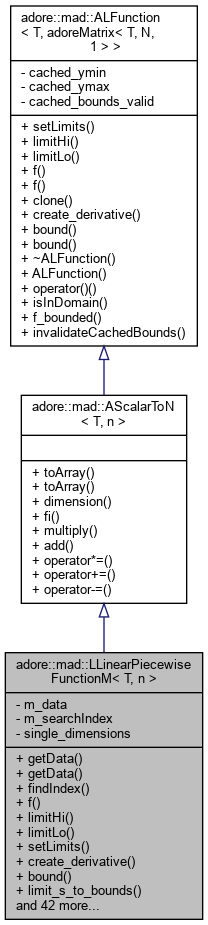
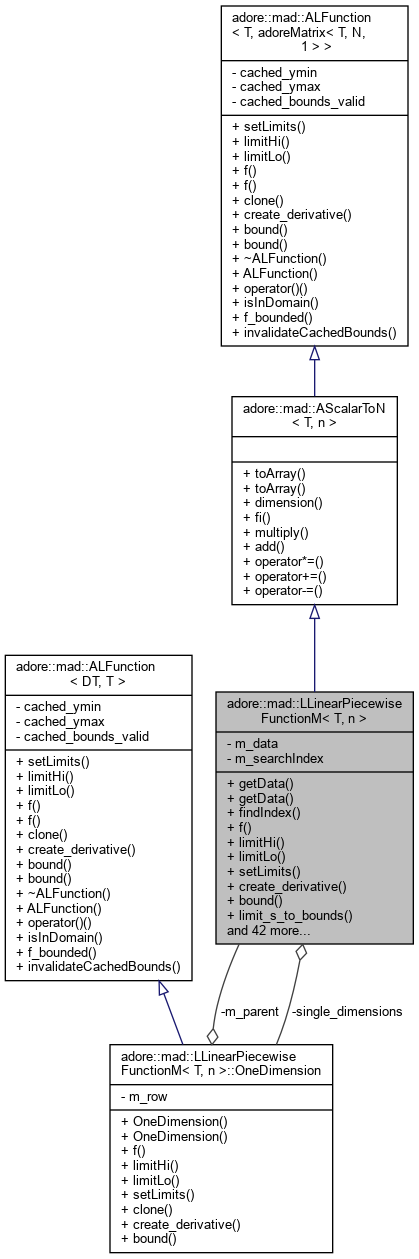
Classes
class	OneDimension

Public Types
typedef adoreMatrix< T, n, 1 >	CT

typedef AScalarToN< T, n >::DT	DT

Public Types inherited from adore::mad::AScalarToN< T, n >
typedef T	DT

typedef adoreMatrix< T, N, 1 >	CT

typedef ALFunction< DT, T >	SUBFUN

Public Member Functions
adoreMatrix< T, n+1, 0 > &	getData ()

const adoreMatrix< T, n+1, 0 > &	getData () const

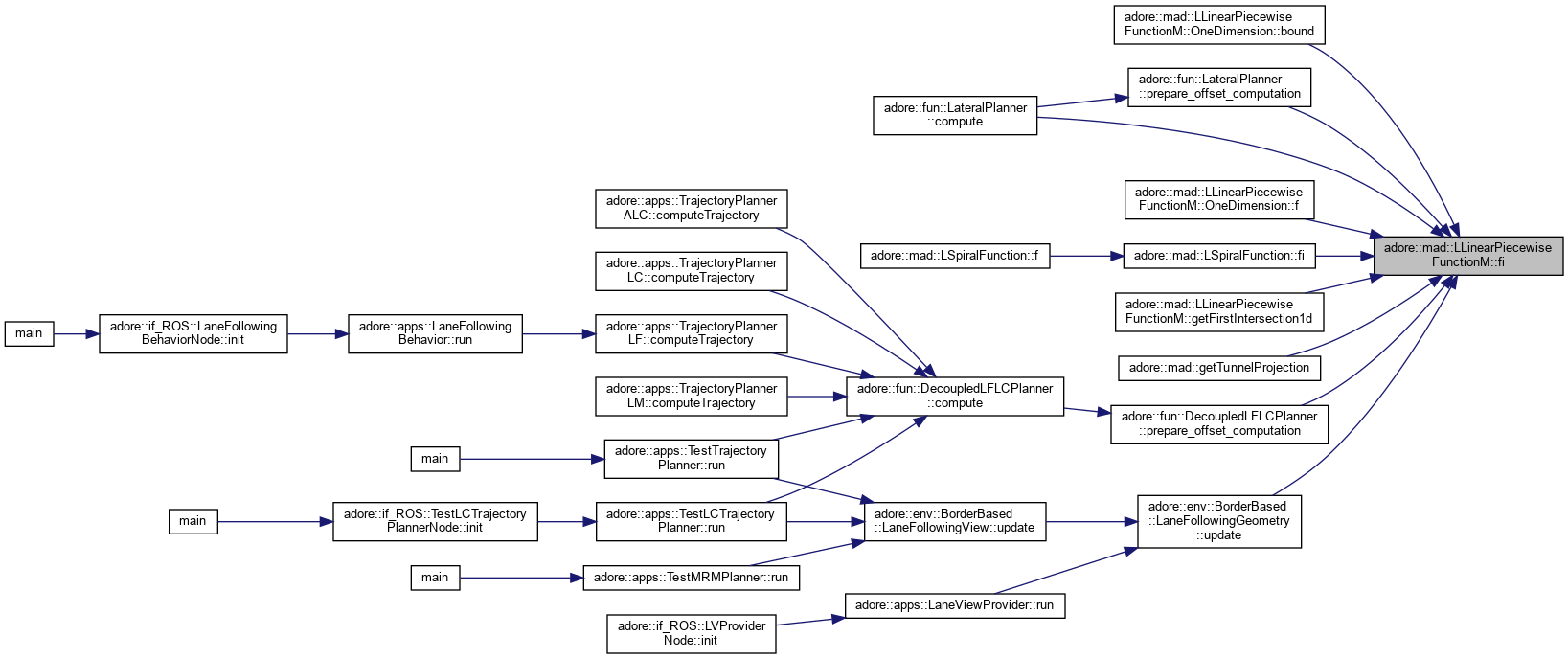
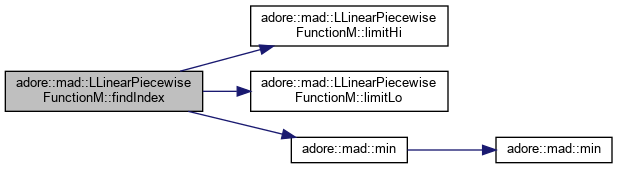
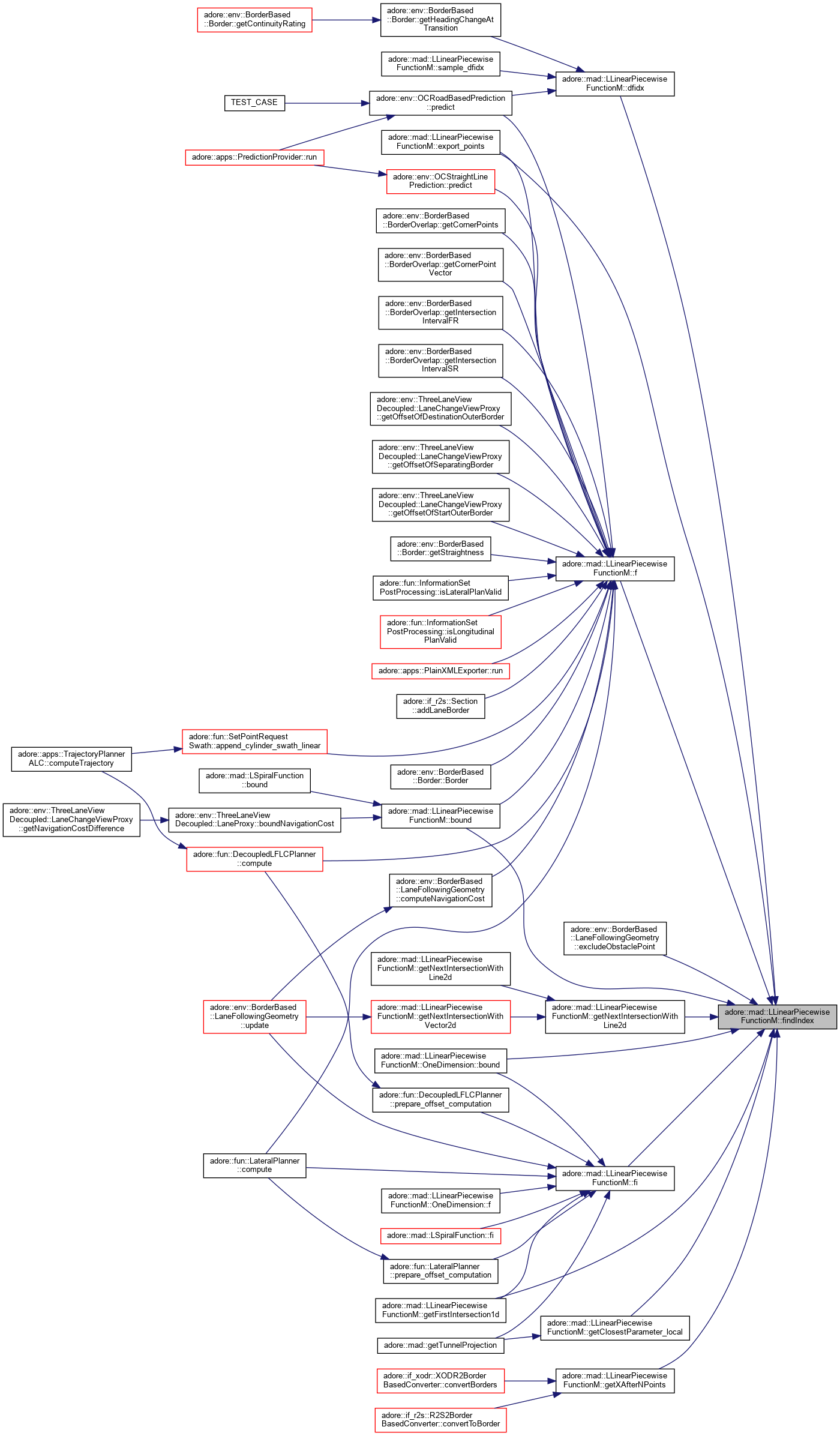
unsigned int	findIndex (DT x, DT precision=0.001) const

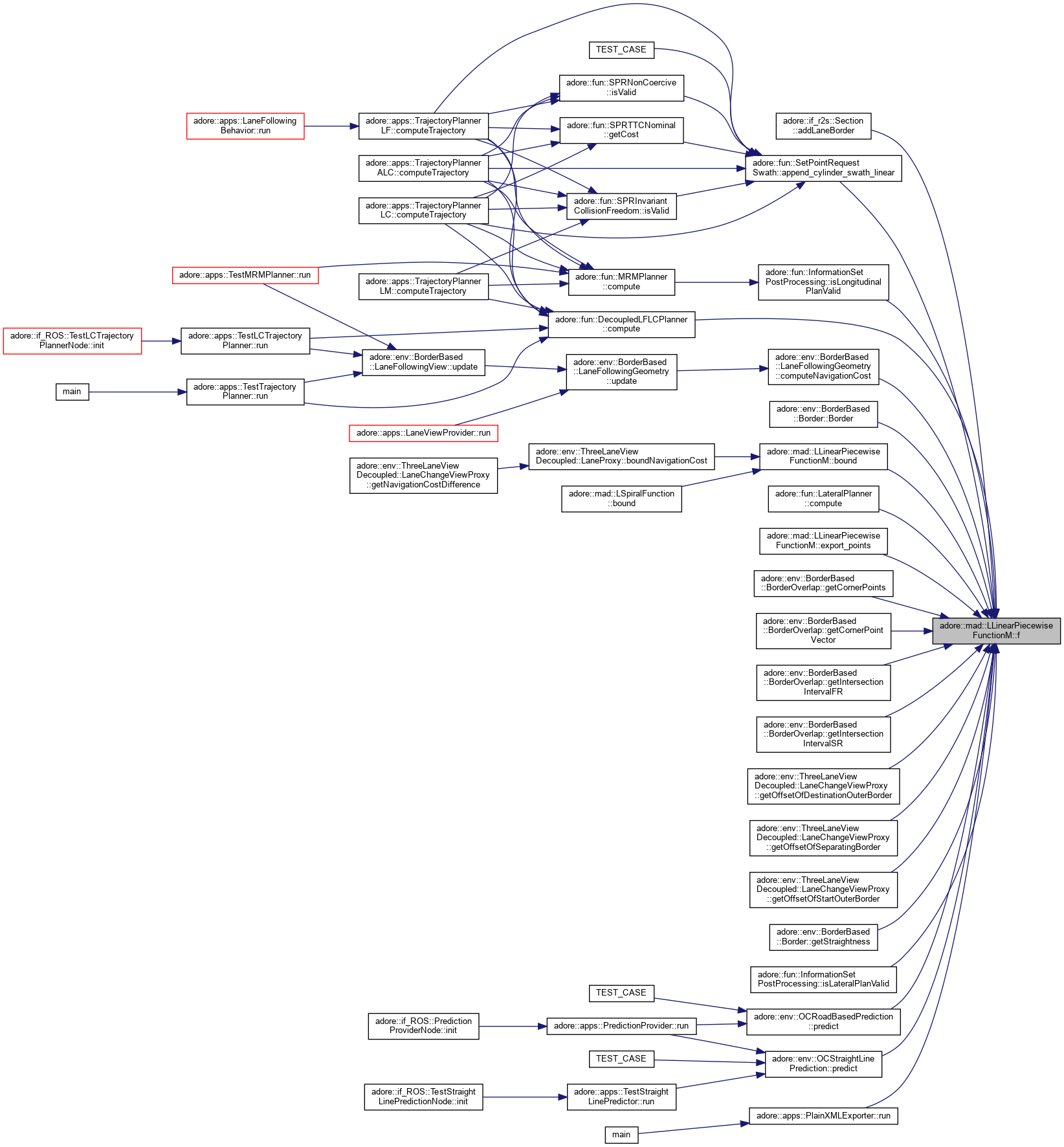
virtual CT	f (DT x) const override

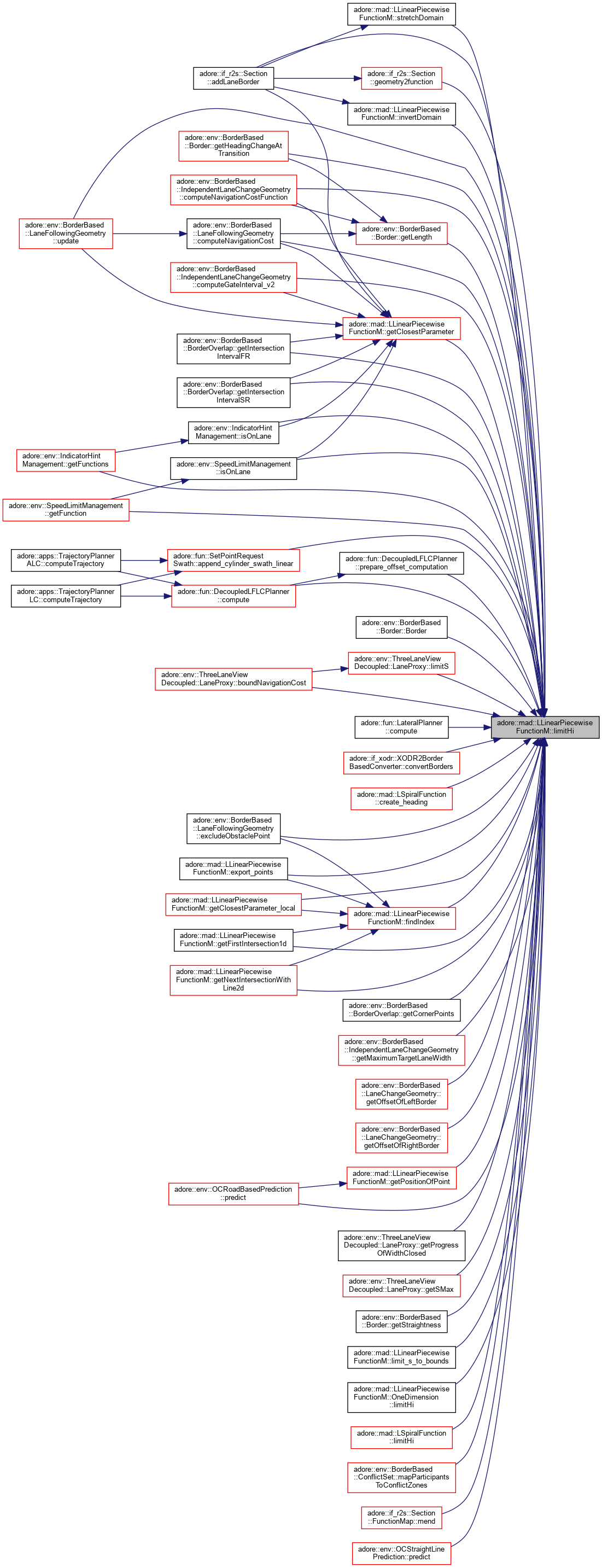
virtual DT	limitHi () const override

virtual DT	limitLo () const override

virtual void	setLimits (DT lo, DT hi) override

virtual ALFunction< DT, CT > *	create_derivative () override

virtual void	bound (const DT &xmin, const DT &xmax, CT &ymin, CT &ymax) override

virtual double	limit_s_to_bounds (double s) const
	shifts s to be in between limitLo and limitHi More...

virtual void	invertDomain ()

virtual void	startDomainAtZero ()

void	shiftDomain (DT dx)

virtual void	stretchDomain (DT x0, DT x1)

void	shiftCodomain (CT dy)

void	shiftCodomain (T dy, int i=0)

void	rotateXY (double angle, double x0=0.0, double y0=0.0)

virtual T	fi (DT x, int row) const override

virtual T	dfidx (DT x, int row)

void	sample_dfidx (DT xvec, T yvec, int count, int row)

virtual ALFunction< DT, T > *	dimension (int i) override

	LLinearPiecewiseFunctionM ()

LLinearPiecewiseFunctionM &	operator= (const LLinearPiecewiseFunctionM &other)

	LLinearPiecewiseFunctionM (const LLinearPiecewiseFunctionM &other)

	LLinearPiecewiseFunctionM (const adoreMatrix< T, n+1, 0 > &data)

	LLinearPiecewiseFunctionM (const adoreMatrix< T, 1, 0 > &xdata, const adoreMatrix< T, n, 0 > &ydata)

	LLinearPiecewiseFunctionM (const int nc, T value)

virtual	~LLinearPiecewiseFunctionM ()

virtual ALFunction< DT, CT > *	clone () override

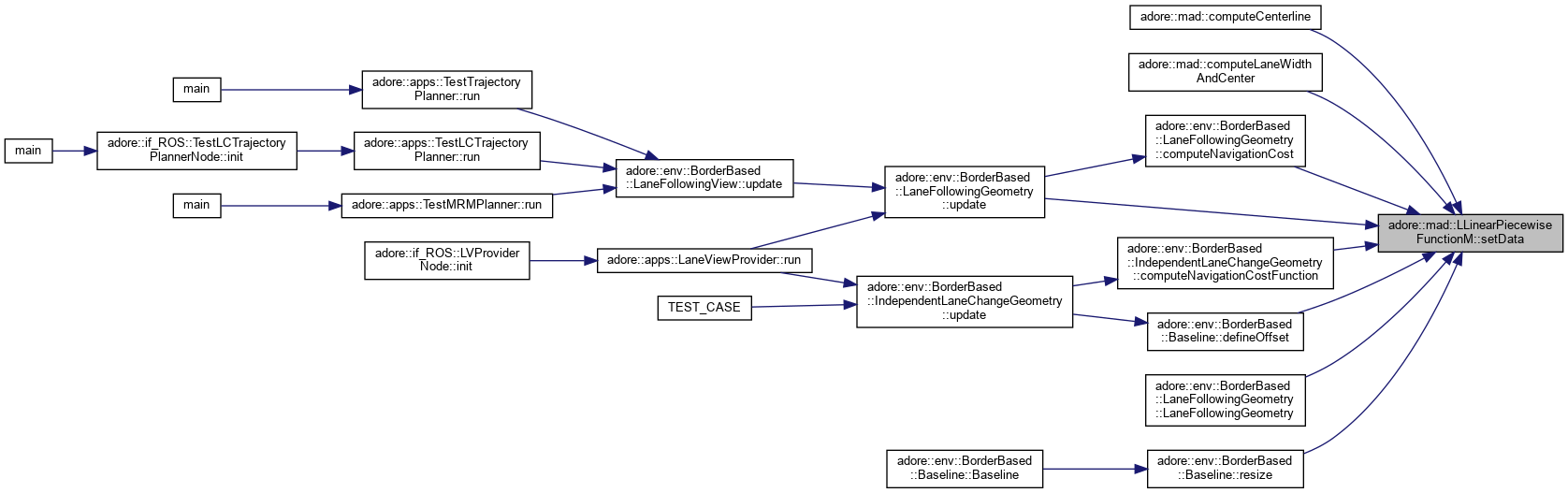
void	setData (const adoreMatrix< T, n+1, 0 > &data)

virtual void	multiply (adoreMatrix< T, 0, 0 > A, int rowi, int rowj) override

virtual void	add (adoreMatrix< T, 0, 1 > b, int rowi, int rowj) override

std::vector< std::pair< T, T > > *	getIntersections2d (LLinearPiecewiseFunctionM< T, n > *other, int dim1, int dim2)

std::vector< std::pair< T, T > > *	getIntersections2d (LLinearPiecewiseFunctionM< T, n > *other)

bool	getFirstIntersection2d (LLinearPiecewiseFunctionM< T, n > *other, int dim1, int dim2, std::pair< T, T > &result)

bool	getFirstIntersection2d (LLinearPiecewiseFunctionM< T, n > *other, std::pair< T, T > &result)

bool	getFirstIntersection1d (T y_cross, int dimension, T &x)

bool	getFirstIntersection1d (T y_cross, T &x)

bool	getFirstIntersection1d (LLinearPiecewiseFunctionM< T, n > *other, int dim, std::pair< T, T > &result)

bool	getNextIntersectionWithLine2d (T x0, T px, T py, T vx, T vy, int d1, int d2, T &x_result, T &distance, bool extend_fringes=false, bool inside_input_line=false)

bool	getNextIntersectionWithLine2d (T x0, T px, T py, T vx, T vy, T &x_result, T &distance, bool extend_fringes=false)

bool	getNextIntersectionWithVector2d (T x0, T px, T py, T vx, T vy, T &x_result, T &distance, T max_distance, bool extend_fringes=false)

int	countIntersectionsWithRay2d (T px, T py, int d1, int d2, T ex, T ey, bool inverted=false)

double	getPositionOfPoint (T px, T py, int d1, int d2, T &d_tangential_min, T &d_normal_min)

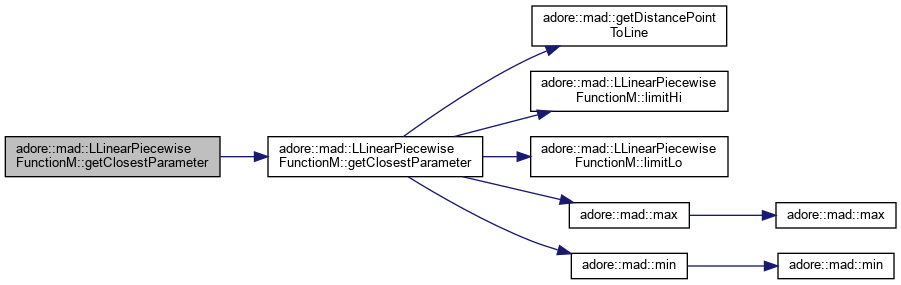
double	getClosestParameter (T px, T py, int d1, int d2, T &n_min) const

double	getClosestParameter_local (T px, T py, int d1, int d2, T x0, T *n_min=nullptr) const

double	getClosestParameter (T px, T py, int d1, int d2) const

bool	isPointEnclosed (LLinearPiecewiseFunctionM< T, n > *other, T px, T py, int d1, int d2, bool invert_this=false, bool invert_other=true)

T	getXAfterNPoints (T xstart, int N)

void	writePointsToArray (int i, int j, T *m)

void	writePointsToArray (int i, int j, int d, T *m)

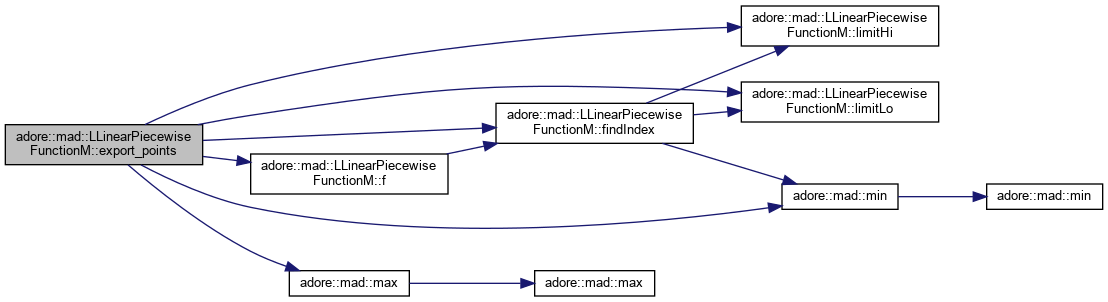
int	export_points (adoreMatrix< double, 0, 0 > &target, double x0, double x1, double precision)

Public Member Functions inherited from adore::mad::AScalarToN< T, n >
void	toArray (DT xvec, T yvec, unsigned int count)

void	toArray (DT xvec, T yvec, unsigned int count, unsigned int row)

virtual T	fi (DT x, int dim) const=0

virtual void	operator*= (adoreMatrix< T, N, N > A)

virtual void	operator+= (adoreMatrix< T, N, 1 > b)

virtual void	operator-= (adoreMatrix< T, N, 1 > b)

Public Member Functions inherited from adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >
virtual void	setLimits (T lo, T hi)=0

virtual adoreMatrix< T, N, 1 >	f (T x) const=0

virtual void	f (T xvec, adoreMatrix< T, N, 1 > yvec, unsigned int count) const

virtual void	bound (const T &xmin, const T &xmax, adoreMatrix< T, N, 1 > &ymin, adoreMatrix< T, N, 1 > &ymax)=0

void	bound (adoreMatrix< T, N, 1 > &ymin, adoreMatrix< T, N, 1 > &ymax)

virtual	~ALFunction ()

	ALFunction ()

const adoreMatrix< T, N, 1 >	operator() (T x) const

bool	isInDomain (T x)

adoreMatrix< T, N, 1 >	f_bounded (T x)

void	invalidateCachedBounds ()

Private Attributes
adoreMatrix< T, n+1, 0 >	m_data

unsigned int	m_searchIndex

OneDimension	single_dimensions [n]

Detailed Description

template<typename T, int n>
class adore::mad::LLinearPiecewiseFunctionM< T, n >

LPiecewiseFunction - a linear interpolation function based on a matrix object, f: DT^1 --> T^n

Member Typedef Documentation

◆ CT

template<typename T , int n>

typedef adoreMatrix<T, n, 1> adore::mad::LLinearPiecewiseFunctionM< T, n >::CT

◆ DT

template<typename T , int n>

typedef AScalarToN<T,n>::DT adore::mad::LLinearPiecewiseFunctionM< T, n >::DT

Constructor & Destructor Documentation

◆ LLinearPiecewiseFunctionM() [1/5]

template<typename T , int n>

adore::mad::LLinearPiecewiseFunctionM< T, n >::LLinearPiecewiseFunctionM ( )

inline

constructor without initialization

◆ LLinearPiecewiseFunctionM() [2/5]

template<typename T , int n>

adore::mad::LLinearPiecewiseFunctionM< T, n >::LLinearPiecewiseFunctionM ( const LLinearPiecewiseFunctionM< T, n > & other )

inline

copy constructor

◆ LLinearPiecewiseFunctionM() [3/5]

template<typename T , int n>

adore::mad::LLinearPiecewiseFunctionM< T, n >::LLinearPiecewiseFunctionM ( const adoreMatrix< T, n+1, 0 > & data )

inline

constructor: initialize with data matrix containing domain and codomain

◆ LLinearPiecewiseFunctionM() [4/5]

template<typename T , int n>

adore::mad::LLinearPiecewiseFunctionM< T, n >::LLinearPiecewiseFunctionM	(	const adoreMatrix< T, 1, 0 > &	xdata,
		const adoreMatrix< T, n, 0 > &	ydata
	)

inline

constructor: initialize with two data matrices containing domain and codomain separately

◆ LLinearPiecewiseFunctionM() [5/5]

template<typename T , int n>

adore::mad::LLinearPiecewiseFunctionM< T, n >::LLinearPiecewiseFunctionM	(	const int	nc,
		T	value
	)

inline

constructor: dynamically sized matrix, initialized with a single value

◆ ~LLinearPiecewiseFunctionM()

template<typename T , int n>

virtual adore::mad::LLinearPiecewiseFunctionM< T, n >::~LLinearPiecewiseFunctionM ( )

inlinevirtual

Member Function Documentation

◆ add()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::add	(	adoreMatrix< T, 0, 1 >	b,
		int	rowi,
		int	rowj
	)

inlineoverridevirtual

apply operation to function sub-dimensions: add vector b to dimensions rowi to rowj

Implements adore::mad::AScalarToN< T, n >.

Here is the caller graph for this function:

◆ bound()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::bound	(	const DT &	xmin,
		const DT &	xmax,
		CT &	ymin,
		CT &	ymax
	)

inlineoverridevirtual

Here is the call graph for this function:

Here is the caller graph for this function:

◆ clone()

template<typename T , int n>

virtual ALFunction<DT, CT>* adore::mad::LLinearPiecewiseFunctionM< T, n >::clone ( )

inlineoverridevirtual

create a copy of child class object - is used for function operations

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

Here is the caller graph for this function:

◆ countIntersectionsWithRay2d()

template<typename T , int n>

int adore::mad::LLinearPiecewiseFunctionM< T, n >::countIntersectionsWithRay2d	(	T	px,
		T	py,
		int	d1,
		int	d2,
		T	ex,
		T	ey,
		bool	inverted = `false`
	)

inline

countIntersectionsWithRay2d - sends a ray starting at px,py in direction of x axis and counts intersections with the lines of this object. dimensions d1 and d2 are used. furthermore, an extension point (ex,ey) is given, which allows to test another line from last point to (ex,ey) The method can be used to test for a point (px,py) whether it is inside the polygon defined by this function object: Unequal number of intersections <=> point is inside specify (ex,ey) as first point of this function object to close the loop of the line sequence. specify (ex,ey) as first point fo next function object to test line sequence consisting of multiple function objects https://en.wikipedia.org/wiki/Point_in_polygon

Here is the caller graph for this function:

◆ create_derivative()

template<typename T , int n>

virtual ALFunction<DT, CT>* adore::mad::LLinearPiecewiseFunctionM< T, n >::create_derivative ( )

inlineoverridevirtual

create a new function object, which is the derivative function

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

◆ dfidx()

template<typename T , int n>

virtual T adore::mad::LLinearPiecewiseFunctionM< T, n >::dfidx	(	DT	x,
		int	row
	)

inlinevirtual

numerical gradient: get a singular value from vector codomain type

Here is the call graph for this function:

Here is the caller graph for this function:

◆ dimension()

template<typename T , int n>

virtual ALFunction<DT, T>* adore::mad::LLinearPiecewiseFunctionM< T, n >::dimension ( int i )

inlineoverridevirtual

get access to a scalar version of this function

Implements adore::mad::AScalarToN< T, n >.

Here is the caller graph for this function:

◆ export_points()

template<typename T , int n>

int adore::mad::LLinearPiecewiseFunctionM< T, n >::export_points	(	adoreMatrix< double, 0, 0 > &	target,
		double	x0,
		double	x1,
		double	precision
	)

inline

export points between x0 and x1 values to a matrix

Here is the call graph for this function:

◆ f()

template<typename T , int n>

virtual CT adore::mad::LLinearPiecewiseFunctionM< T, n >::f ( DT x ) const

inlineoverridevirtual

Here is the call graph for this function:

Here is the caller graph for this function:

◆ fi()

template<typename T , int n>

virtual T adore::mad::LLinearPiecewiseFunctionM< T, n >::fi	(	DT	x,
		int	row
	)		const

inlineoverridevirtual

get a singular value from vector codomain type

Here is the call graph for this function:

Here is the caller graph for this function:

◆ findIndex()

template<typename T , int n>

unsigned int adore::mad::LLinearPiecewiseFunctionM< T, n >::findIndex	(	DT	x,
		DT	precision = `0.001`
	)		const

inline

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getClosestParameter() [1/2]

template<typename T , int n>

double adore::mad::LLinearPiecewiseFunctionM< T, n >::getClosestParameter	(	T	px,
		T	py,
		int	d1,
		int	d2
	)		const

inline

Here is the call graph for this function:

◆ getClosestParameter() [2/2]

template<typename T , int n>

double adore::mad::LLinearPiecewiseFunctionM< T, n >::getClosestParameter	(	T	px,
		T	py,
		int	d1,
		int	d2,
		T &	n_min
	)		const

inline

returns the parameter of the function value at dimensions d1,d2 with closest euclidean distance to px,py

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getClosestParameter_local()

template<typename T , int n>

double adore::mad::LLinearPiecewiseFunctionM< T, n >::getClosestParameter_local	(	T	px,
		T	py,
		int	d1,
		int	d2,
		T	x0,
		T *	n_min = `nullptr`
	)		const

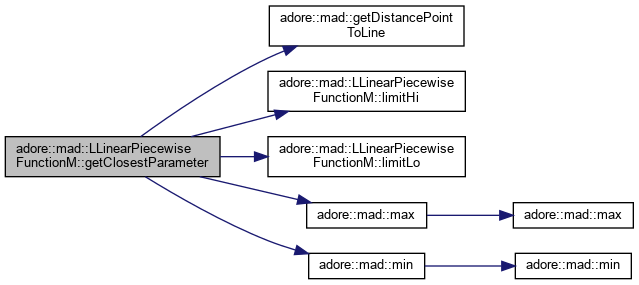
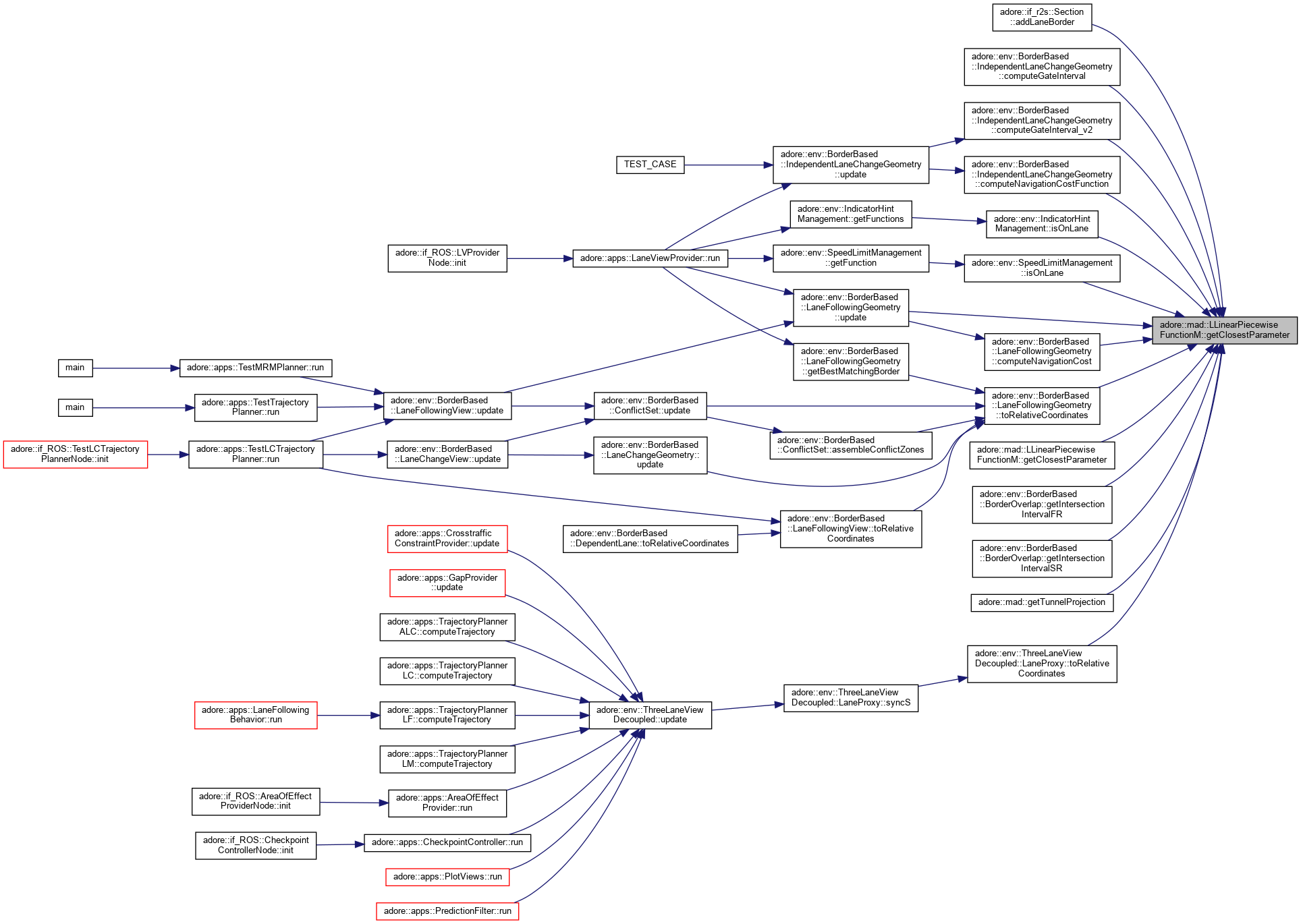
inline

returns the parameter of the function value at dimensions d1,d2 with closest euclidean distance to px,py, local search starting at x0

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getData() [1/2]

template<typename T , int n>

adoreMatrix<T, n + 1, 0>& adore::mad::LLinearPiecewiseFunctionM< T, n >::getData ( )

inline

◆ getData() [2/2]

template<typename T , int n>

const adoreMatrix<T, n + 1, 0>& adore::mad::LLinearPiecewiseFunctionM< T, n >::getData ( ) const

inline

◆ getFirstIntersection1d() [1/3]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getFirstIntersection1d	(	LLinearPiecewiseFunctionM< T, n > *	other,
		int	dim,
		std::pair< T, T > &	result
	)

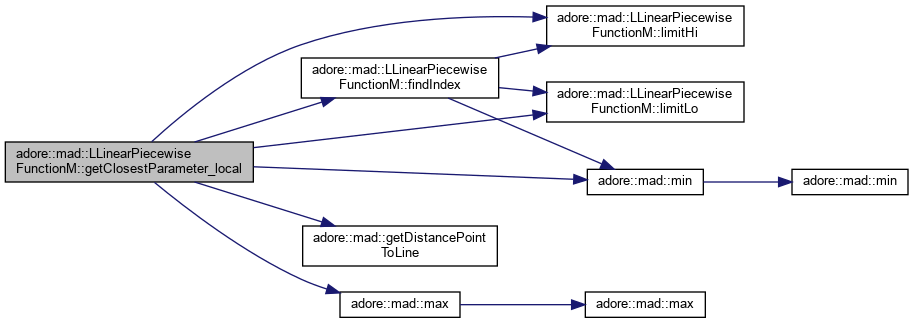
inline

one dimensional intersection test

Parameters

dim	dimension to be tested
result	first intersection: domain values of intersection point

Returns: true if other and this intersect in dimension dim

Here is the call graph for this function:

◆ getFirstIntersection1d() [2/3]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getFirstIntersection1d	(	T	y_cross,
		int	dimension,
		T &	x
	)

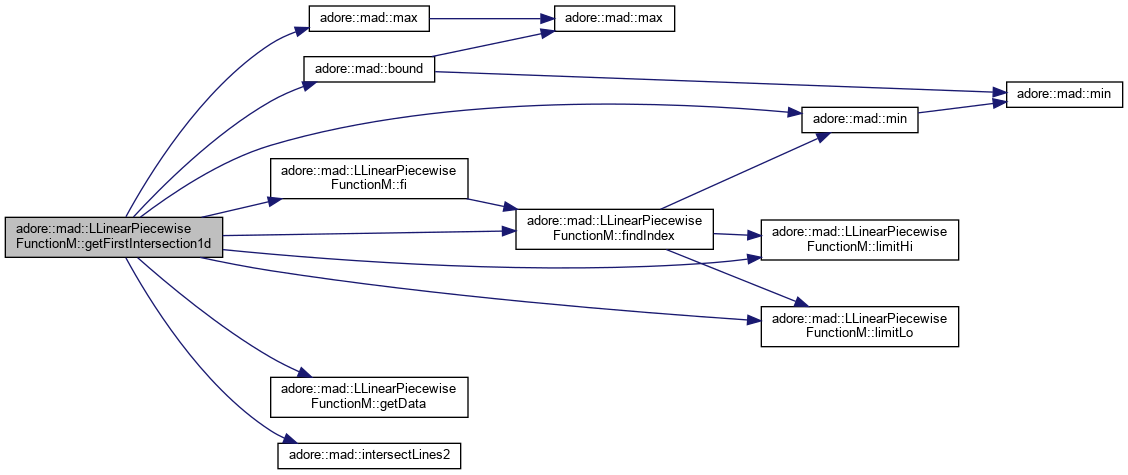
inline

getFirstIntersection1d - zero crossing test returns true, if a "zero" crossing happens tests for crossing y_cross value in dimension "dimension" the x coordinate is written in x, if a crossing occurs

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getFirstIntersection1d() [3/3]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getFirstIntersection1d	(	T	y_cross,
		T &	x
	)

inline

Here is the call graph for this function:

◆ getFirstIntersection2d() [1/2]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getFirstIntersection2d	(	LLinearPiecewiseFunctionM< T, n > *	other,
		int	dim1,
		int	dim2,
		std::pair< T, T > &	result
	)

inline

computes the first intersection between two line sequences, with first seen from perspective of this returns true if an intersection was found and then writes domain values for intersection into result, with first for this and second for other.

Here is the caller graph for this function:

◆ getFirstIntersection2d() [2/2]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getFirstIntersection2d	(	LLinearPiecewiseFunctionM< T, n > *	other,
		std::pair< T, T > &	result
	)

inline

Here is the call graph for this function:

◆ getIntersections2d() [1/2]

template<typename T , int n>

std::vector<std::pair<T, T> >* adore::mad::LLinearPiecewiseFunctionM< T, n >::getIntersections2d ( LLinearPiecewiseFunctionM< T, n > * other )

inline

Here is the call graph for this function:

◆ getIntersections2d() [2/2]

template<typename T , int n>

std::vector<std::pair<T, T> >* adore::mad::LLinearPiecewiseFunctionM< T, n >::getIntersections2d	(	LLinearPiecewiseFunctionM< T, n > *	other,
		int	dim1,
		int	dim2
	)

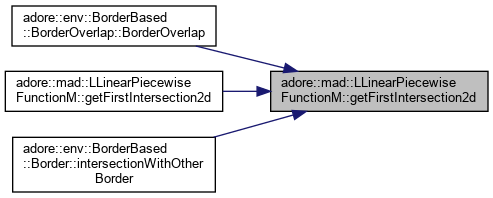
inline

test whether this and other intersect in dimension d1 and d2 - a vector of pairs of x-values (domain) is returned, with one entry for every intersection and the first entry in a pair for this and the second entry for other

Here is the caller graph for this function:

◆ getNextIntersectionWithLine2d() [1/2]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getNextIntersectionWithLine2d	(	T	x0,
		T	px,
		T	py,
		T	vx,
		T	vy,
		int	d1,
		int	d2,
		T &	x_result,
		T &	distance,
		bool	extend_fringes = `false`,
		bool	inside_input_line = `false`
	)

inline

getNextIntersectionWithLine2d - returns the next x-position after x0, at which the line with start (px,py) and direction (vx,vy) intersects this in dimensions d1,d2. returns true if an intersection was found after x0 sets x_result to the parametrization of this at which intersection occurs, e.g. ip = f_d1d2(x_result); sets distance to the parameter required to achieve the intersection point via the given line, e.g. ip=(px,py) + (vx,vy)*distance; extend_fringes - if extend_fringes is true, the function is extrapolated in order to provide intersection points beyond its domain

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getNextIntersectionWithLine2d() [2/2]

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getNextIntersectionWithLine2d	(	T	x0,
		T	px,
		T	py,
		T	vx,
		T	vy,
		T &	x_result,
		T &	distance,
		bool	extend_fringes = `false`
	)

inline

Here is the call graph for this function:

◆ getNextIntersectionWithVector2d()

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::getNextIntersectionWithVector2d	(	T	x0,
		T	px,
		T	py,
		T	vx,
		T	vy,
		T &	x_result,
		T &	distance,
		T	max_distance,
		bool	extend_fringes = `false`
	)

inline

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getPositionOfPoint()

template<typename T , int n>

double adore::mad::LLinearPiecewiseFunctionM< T, n >::getPositionOfPoint	(	T	px,
		T	py,
		int	d1,
		int	d2,
		T &	d_tangential_min,
		T &	d_normal_min
	)

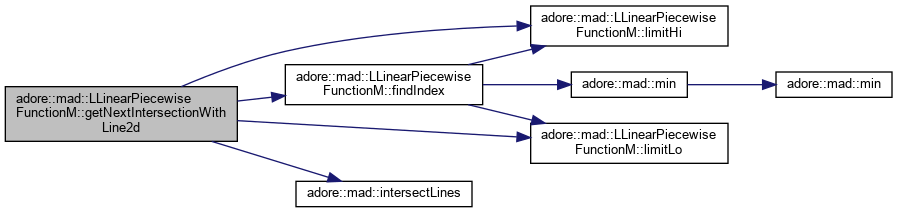
inline

getPositionOfPoint - returns best-fit d_tangential and d_normal: if d_tangential>1 or d_tangential<0, the point is not projected onto function interval the according function parameter for given point is returned

Here is the call graph for this function:

Here is the caller graph for this function:

◆ getXAfterNPoints()

template<typename T , int n>

T adore::mad::LLinearPiecewiseFunctionM< T, n >::getXAfterNPoints	(	T	xstart,
		int	N
	)

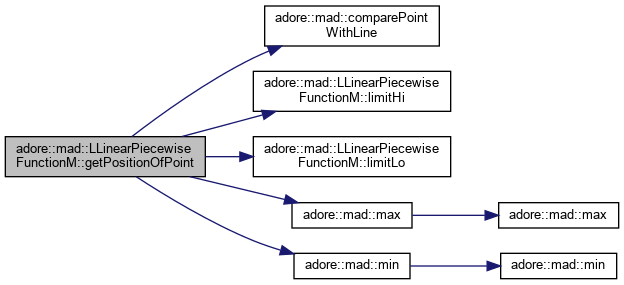
inline

returns the x-value if going forward N points

Here is the call graph for this function:

Here is the caller graph for this function:

◆ invertDomain()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::invertDomain ( )

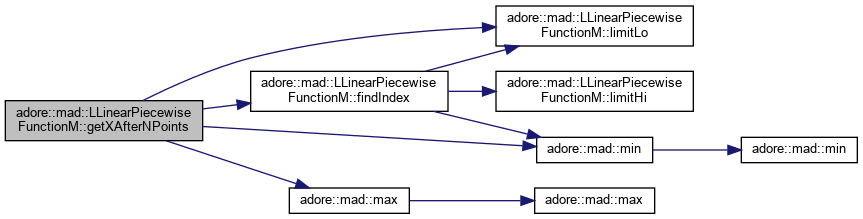
inlinevirtual

retains the overall domain between lo and hi, but inverts direction in between

Here is the call graph for this function:

Here is the caller graph for this function:

◆ isPointEnclosed()

template<typename T , int n>

bool adore::mad::LLinearPiecewiseFunctionM< T, n >::isPointEnclosed	(	LLinearPiecewiseFunctionM< T, n > *	other,
		T	px,
		T	py,
		int	d1,
		int	d2,
		bool	invert_this = `false`,
		bool	invert_other = `true`
	)

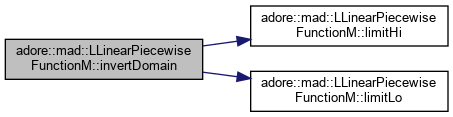
inline

isPointEnclosed - Returns true if a point x is enclosed by the two line segments this, other and the lines connecting this' and other's endpoints. This and other have to form a counter clockwise loop if their endpoints are connected, so that the interior of the loop is well defined. If this and other do not form a ccw loop, use invert_this or invert_other to temporarily change directions, to achieve ccw loop. https://en.wikipedia.org/wiki/Point_in_polygon

Here is the call graph for this function:

Here is the caller graph for this function:

◆ limit_s_to_bounds()

template<typename T , int n>

virtual double adore::mad::LLinearPiecewiseFunctionM< T, n >::limit_s_to_bounds ( double s ) const

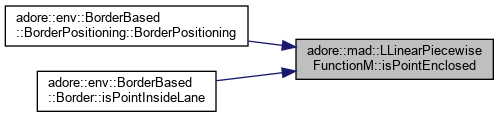
inlinevirtual

shifts s to be in between limitLo and limitHi

Parameters

s

Returns: double

See also: limitLo(), limitHi()

Here is the call graph for this function:

◆ limitHi()

template<typename T , int n>

virtual DT adore::mad::LLinearPiecewiseFunctionM< T, n >::limitHi ( ) const

inlineoverridevirtual

query upper limit of the domain

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

Here is the caller graph for this function:

◆ limitLo()

template<typename T , int n>

virtual DT adore::mad::LLinearPiecewiseFunctionM< T, n >::limitLo ( ) const

inlineoverridevirtual

lower limit of the domain

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

◆ multiply()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::multiply	(	adoreMatrix< T, 0, 0 >	A,
		int	rowi,
		int	rowj
	)

inlineoverridevirtual

apply operation to function sub-dimensions: multiply with matrix of lower dimension in range rowi to rowj, with A.nc==A.nr==rowj-rowi+1

Implements adore::mad::AScalarToN< T, n >.

Here is the caller graph for this function:

◆ operator=()

template<typename T , int n>

LLinearPiecewiseFunctionM& adore::mad::LLinearPiecewiseFunctionM< T, n >::operator= ( const LLinearPiecewiseFunctionM< T, n > & other )

inline

◆ rotateXY()

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::rotateXY	(	double	angle,
		double	x0 = `0.0`,
		double	y0 = `0.0`
	)

inline

rotate codomain in 2D

Here is the call graph for this function:

Here is the caller graph for this function:

◆ sample_dfidx()

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::sample_dfidx	(	DT *	xvec,
		T *	yvec,
		int	count,
		int	row
	)

inline

sapmle a range of x values and evaluate gradient for one row of the vector only

Here is the call graph for this function:

◆ setData()

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::setData ( const adoreMatrix< T, n+1, 0 > & data )

inline

set the domain and codomain from data matrix

Here is the caller graph for this function:

◆ setLimits()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::setLimits	(	DT	lo,
		DT	hi
	)

inlineoverridevirtual

Here is the caller graph for this function:

◆ shiftCodomain() [1/2]

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::shiftCodomain ( CT dy )

inline

shifts the codomain of the function (move graph up or down)

Here is the caller graph for this function:

◆ shiftCodomain() [2/2]

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::shiftCodomain	(	T	dy,
		int	i = `0`
	)

inline

shift a single dimension of the codomain

◆ shiftDomain()

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::shiftDomain ( DT dx )

inline

shifts the domain of the function by dx (move graph left or right)

Here is the caller graph for this function:

◆ startDomainAtZero()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::startDomainAtZero ( )

inlinevirtual

shifts the function in such a way that the domain starts at 0

Here is the call graph for this function:

◆ stretchDomain()

template<typename T , int n>

virtual void adore::mad::LLinearPiecewiseFunctionM< T, n >::stretchDomain	(	DT	x0,
		DT	x1
	)

inlinevirtual

stretches domain to fit interval [x0,x1]

Here is the call graph for this function:

Here is the caller graph for this function:

◆ writePointsToArray() [1/2]

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::writePointsToArray	(	int	i,
		int	j,
		int	d,
		T *	m
	)

inline

writes j-i points into an array m, for dimension d, using the natural stepsize

◆ writePointsToArray() [2/2]

template<typename T , int n>

void adore::mad::LLinearPiecewiseFunctionM< T, n >::writePointsToArray	(	int	i,
		int	j,
		T *	m
	)

inline

writes j-i points into an array m, using the natural stepsize

Member Data Documentation

◆ m_data

template<typename T , int n>

adoreMatrix<T, n + 1, 0> adore::mad::LLinearPiecewiseFunctionM< T, n >::m_data

private

◆ m_searchIndex

template<typename T , int n>

unsigned int adore::mad::LLinearPiecewiseFunctionM< T, n >::m_searchIndex

mutableprivate

◆ single_dimensions

template<typename T , int n>

OneDimension adore::mad::LLinearPiecewiseFunctionM< T, n >::single_dimensions[n]

private

The documentation for this class was generated from the following file:

/home/fascar/temp/adore/libadore/libadore/adore/mad/include/adore/mad/llinearpiecewisefunction.h

Classes

Public Types

Public Member Functions

Private Attributes

Detailed Description

template<typename T, int n> class adore::mad::LLinearPiecewiseFunctionM< T, n >

Member Typedef Documentation

◆ CT

◆ DT

Constructor & Destructor Documentation

◆ LLinearPiecewiseFunctionM() [1/5]

◆ LLinearPiecewiseFunctionM() [2/5]

◆ LLinearPiecewiseFunctionM() [3/5]

◆ LLinearPiecewiseFunctionM() [4/5]

◆ LLinearPiecewiseFunctionM() [5/5]

◆ ~LLinearPiecewiseFunctionM()

Member Function Documentation

◆ add()

◆ bound()

◆ clone()

◆ countIntersectionsWithRay2d()

◆ create_derivative()

◆ dfidx()

◆ dimension()

◆ export_points()

◆ f()

◆ fi()

◆ findIndex()

◆ getClosestParameter() [1/2]

◆ getClosestParameter() [2/2]

◆ getClosestParameter_local()

◆ getData() [1/2]

◆ getData() [2/2]

◆ getFirstIntersection1d() [1/3]

◆ getFirstIntersection1d() [2/3]

◆ getFirstIntersection1d() [3/3]

◆ getFirstIntersection2d() [1/2]

◆ getFirstIntersection2d() [2/2]

◆ getIntersections2d() [1/2]

◆ getIntersections2d() [2/2]

◆ getNextIntersectionWithLine2d() [1/2]

◆ getNextIntersectionWithLine2d() [2/2]

◆ getNextIntersectionWithVector2d()

◆ getPositionOfPoint()

◆ getXAfterNPoints()

◆ invertDomain()

◆ isPointEnclosed()

◆ limit_s_to_bounds()

◆ limitHi()

◆ limitLo()

◆ multiply()

◆ operator=()

◆ rotateXY()

◆ sample_dfidx()

◆ setData()

◆ setLimits()

◆ shiftCodomain() [1/2]

◆ shiftCodomain() [2/2]

◆ shiftDomain()

◆ startDomainAtZero()

◆ stretchDomain()

◆ writePointsToArray() [1/2]

◆ writePointsToArray() [2/2]

Member Data Documentation

◆ m_data

◆ m_searchIndex

◆ single_dimensions

template<typename T, int n>
class adore::mad::LLinearPiecewiseFunctionM< T, n >