#include <lpolynomial.h>

Inheritance diagram for adore::mad::LPolynomialM< T, N, M >:

Collaboration diagram for adore::mad::LPolynomialM< T, N, M >:

Classes
class	OneDimension

Public Types
typedef adoreMatrix< T, N, 1 >	CT

typedef T	DT

typedef ALFunction< T, T >	SUBFUN

Public Types inherited from adore::mad::AScalarToN< T, N >
typedef T	DT

typedef adoreMatrix< T, N, 1 >	CT

typedef ALFunction< DT, T >	SUBFUN

Public Member Functions
	LPolynomialM (const adoreMatrix< T, N, M+1 > &data, T xmin, T xmax)

virtual CT	f (DT x) const override

virtual DT	limitHi () const override

virtual DT	limitLo () const override

virtual void	setLimits (DT lo, DT hi) override

virtual ALFunction< DT, CT > *	clone () override

virtual ALFunction< DT, CT > *	create_derivative () override

virtual void	bound (const DT &xmin, const DT &xmax, CT &ymin, CT &ymax) override

virtual T	fi (T x, int row) const override

virtual SUBFUN *	dimension (int i) override

virtual void	multiply (adoreMatrix< T, 0, 0 > A, int rowi, int rowj) override

virtual void	add (adoreMatrix< T, 0, 1 > b, int rowi, int rowj) override

Public Member Functions inherited from adore::mad::AScalarToN< T, N >
void	toArray (DT xvec, T yvec, unsigned int count)

void	toArray (DT xvec, T yvec, unsigned int count, unsigned int row)

virtual void	operator*= (adoreMatrix< T, N, N > A)

virtual void	operator+= (adoreMatrix< T, N, 1 > b)

virtual void	operator-= (adoreMatrix< T, N, 1 > b)

Public Member Functions inherited from adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >
virtual void	f (T xvec, adoreMatrix< T, N, 1 > yvec, unsigned int count) const

void	bound (adoreMatrix< T, N, 1 > &ymin, adoreMatrix< T, N, 1 > &ymax)

virtual	~ALFunction ()

	ALFunction ()

const adoreMatrix< T, N, 1 >	operator() (T x) const

bool	isInDomain (T x)

adoreMatrix< T, N, 1 >	f_bounded (T x)

void	invalidateCachedBounds ()

Private Attributes
adoreMatrix< T, N, M+1 >	m_data

T	m_xmin

T	m_xmax

OneDimension	single_dimensions [N]

Detailed Description

template<typename T, int N, int M>
class adore::mad::LPolynomialM< T, N, M >

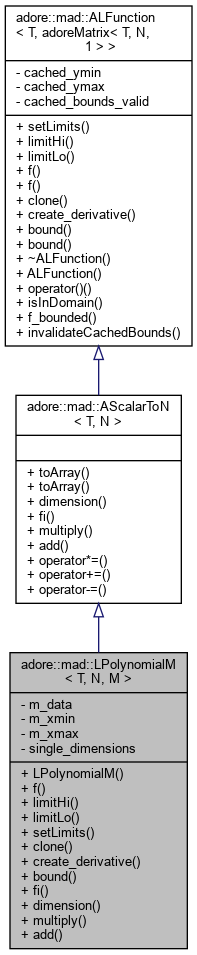
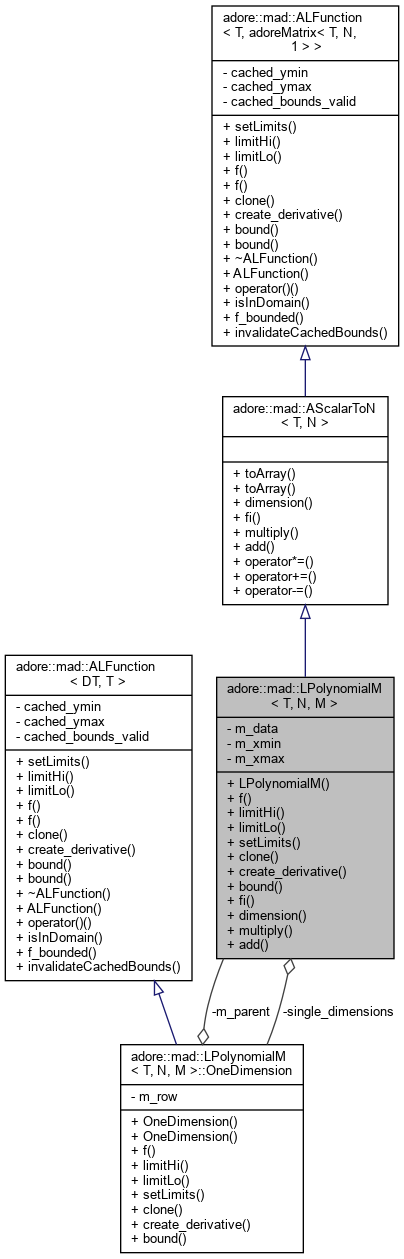
LPolynomialM - a polynomial with vector valued y: Mapping T->adoreMatrix<T,N,1>

Member Typedef Documentation

◆ CT

template<typename T , int N, int M>

typedef adoreMatrix<T, N, 1> adore::mad::LPolynomialM< T, N, M >::CT

◆ DT

template<typename T , int N, int M>

typedef T adore::mad::LPolynomialM< T, N, M >::DT

◆ SUBFUN

template<typename T , int N, int M>

typedef ALFunction<T, T> adore::mad::LPolynomialM< T, N, M >::SUBFUN

Constructor & Destructor Documentation

◆ LPolynomialM()

template<typename T , int N, int M>

adore::mad::LPolynomialM< T, N, M >::LPolynomialM	(	const adoreMatrix< T, N, M+1 > &	data,
		T	xmin,
		T	xmax
	)

inline

Member Function Documentation

◆ add()

template<typename T , int N, int M>

virtual void adore::mad::LPolynomialM< T, N, M >::add	(	adoreMatrix< T, 0, 1 >	b,
		int	rowi,
		int	rowj
	)

inlineoverridevirtual

apply operation to function subdimensions: add a vector to rowi to rowj

Implements adore::mad::AScalarToN< T, N >.

Here is the caller graph for this function:

◆ bound()

template<typename T , int N, int M>

virtual void adore::mad::LPolynomialM< T, N, M >::bound	(	const DT &	xmin,
		const DT &	xmax,
		CT &	ymin,
		CT &	ymax
	)

inlineoverridevirtual

bound function values in the x-range defined by the hypercube between corner points lower left xmin and upper right xmax

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

◆ clone()

template<typename T , int N, int M>

virtual ALFunction<DT, CT>* adore::mad::LPolynomialM< T, N, M >::clone ( )

inlineoverridevirtual

create a copy of child class object - is used for function operations

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

◆ create_derivative()

template<typename T , int N, int M>

virtual ALFunction<DT, CT>* adore::mad::LPolynomialM< T, N, M >::create_derivative ( )

inlineoverridevirtual

create a new function object, which is the derivative function

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

Here is the caller graph for this function:

◆ dimension()

template<typename T , int N, int M>

virtual SUBFUN* adore::mad::LPolynomialM< T, N, M >::dimension ( int i )

inlineoverridevirtual

gives access to a scalar sub-function. does not create a new object, so use clone() to get your own instance of the subfunction.

Implements adore::mad::AScalarToN< T, N >.

◆ f()

template<typename T , int N, int M>

virtual CT adore::mad::LPolynomialM< T, N, M >::f ( DT x ) const

inlineoverridevirtual

function evaluation returns y of codomain type CT for a value x of domain type DT

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

◆ fi()

template<typename T , int N, int M>

virtual T adore::mad::LPolynomialM< T, N, M >::fi	(	T	x,
		int	dim
	)		const

inlineoverridevirtual

scalar evaluation of function: for y-component dim

Implements adore::mad::AScalarToN< T, N >.

Here is the caller graph for this function:

◆ limitHi()

template<typename T , int N, int M>

virtual DT adore::mad::LPolynomialM< T, N, M >::limitHi ( ) const

inlineoverridevirtual

query upper limit of the domain

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

Here is the caller graph for this function:

◆ limitLo()

template<typename T , int N, int M>

virtual DT adore::mad::LPolynomialM< T, N, M >::limitLo ( ) const

inlineoverridevirtual

lower limit of the domain

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

Here is the caller graph for this function:

◆ multiply()

template<typename T , int N, int M>

virtual void adore::mad::LPolynomialM< T, N, M >::multiply	(	adoreMatrix< T, 0, 0 >	A,
		int	rowi,
		int	rowj
	)

inlineoverridevirtual

apply operation to function sub-dimensions: multiply with matrix of lower dimension in range rowi to rowj, with A.nc==A.nr==rowj-rowi+1

Implements adore::mad::AScalarToN< T, N >.

Here is the caller graph for this function:

◆ setLimits()

template<typename T , int N, int M>

virtual void adore::mad::LPolynomialM< T, N, M >::setLimits	(	DT	lo,
		DT	hi
	)

inlineoverridevirtual

reduce or increase the limit of the function, without changing y

Implements adore::mad::ALFunction< T, adoreMatrix< T, N, 1 > >.

Member Data Documentation

◆ m_data

template<typename T , int N, int M>

adoreMatrix<T, N, M + 1> adore::mad::LPolynomialM< T, N, M >::m_data

private

◆ m_xmax

template<typename T , int N, int M>

T adore::mad::LPolynomialM< T, N, M >::m_xmax

private

◆ m_xmin

template<typename T , int N, int M>

T adore::mad::LPolynomialM< T, N, M >::m_xmin

private

◆ single_dimensions

template<typename T , int N, int M>

OneDimension adore::mad::LPolynomialM< T, N, M >::single_dimensions[N]

private

The documentation for this class was generated from the following file:

/home/fascar/temp/adore/libadore/libadore/adore/mad/include/adore/mad/lpolynomial.h

Classes

Public Types

Public Member Functions

Private Attributes

Detailed Description

template<typename T, int N, int M> class adore::mad::LPolynomialM< T, N, M >

Member Typedef Documentation

◆ CT

◆ DT

◆ SUBFUN

Constructor & Destructor Documentation

◆ LPolynomialM()

Member Function Documentation

◆ add()

◆ bound()

◆ clone()

◆ create_derivative()

◆ dimension()

◆ f()

◆ fi()

◆ limitHi()

◆ limitLo()

◆ multiply()

◆ setLimits()

Member Data Documentation

◆ m_data

◆ m_xmax

◆ m_xmin

◆ single_dimensions

template<typename T, int N, int M>
class adore::mad::LPolynomialM< T, N, M >